Wartości




 
Dziedzina
  • Funkcje sinus i cosinus określone są dla każdej liczby rzeczywistej.

  • Tangens jest określony w zbiorze powstałym ze zbioru wszystkich liczb rzeczywistych przez usunięcie liczb mających postać \tfrac{\pi}{2}+k\pi\;, gdzie k\; jest liczbą całkowitą.


  • Cotangens jest określony w zbiorze wszystkich liczb rzeczywistych poza liczbami postaci k\pi\;, gdzie k\; jest liczbą całkowitą.
Przeciwdziedzina
  • Sinus i cosinus są ograniczone: przyjmują wartości z przedziału [-1;1]\;. Tangens i cotangens przyjmują dowolne wartości rzeczywiste.
Ekstrema
  • Maksymalną wartość, w obu przypadkach 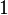1\;, sinus przyjmuje w punktach x=\tfrac{\pi}{2}+2k\pi\;, a cosinus w punktach x=2k\pi\;, gdzie k\; jest całkowita.

    •
  • Minimalną wartość, dla obu funkcji -1\;, sinus przyjmuje w punktach x=-\tfrac{\pi}{2}+2k\pi\;, a cosinus w punktach x=\pi+2k\pi\;, gdzie k\; jest całkowita.
Miejsca zerowe
  • Miejscami zerowymi sinusa i tangensa są punkty postaci x=k\pi\;, gdzie k\; jest całkowita.
  • Miejscami zerowymi cosinusa i cotangensa są punkty postaci x=\tfrac{\pi}{2}+k\pi\;, gdzie k\; jest całkowita.

Parzystość i nieparzystość
  • Funkcje sinus, tangens, cotangens są nieparzyste, a funkcje cosinus parzyste:
    \begin{array}{l l} \sin (-x) = -\sin x & \cos (-x) = \cos x \\ \mbox{tg}(-x) = -\mbox{tg}\ x & \mbox{ctg} (-x) = -\mbox{ctg}\ x \\ \mbox{sec} (-x) = \mbox{sec}\ x & \mbox{csc} (-x) = -\mbox{csc}\ x\end{array}
Okresowość
  • Funkcje trygonometryczne są funkcjami okresowymi. Okresem podstawowym sinusa, cosinusa  jest liczba 2\pi\; a tangensa i cotangensa \pi\;:
    \begin{array}{l l}\sin x = \sin(x + 2k\pi) & \cos x = \cos(x + 2k\pi) \\ \mbox{tg}\ x = \mbox{tg} (x + k\pi) & \mbox{ctg}\ x = \mbox{ctg} (x + k\pi) \\ \mbox{sec}\ x = \mbox{sec} (x + 2k\pi) & \mbox{csc}\ x = \mbox{csc} (x + 2k\pi)\end{array}
gdzie k\; jest liczbą całkowitą.
Subskrybuj: Posty (Atom)